GBDT算法
在上篇推文中,小编介绍了集成学习家族的一个重要算法Adaboost,今天我们来看一看集成学习家族中另一个更加常用的的算法GBDT。
GBDT概述
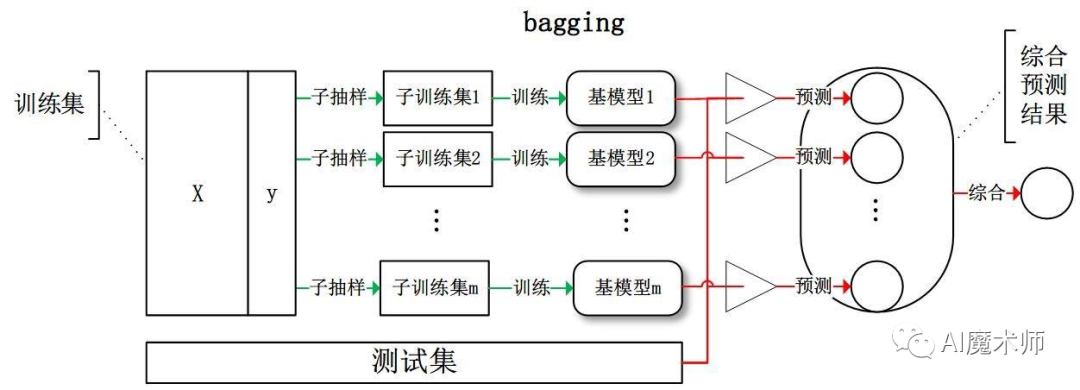
集成学习不是单独的机器学习方法,而是通过构建并结合多个机器学习器来完成任务,集成学习可以用于分类问题集成、回归问题集成、特征选取集成、异常点检测集成等方面。其思想是对于训练数据集,我们通过训练若干个个体学习器,通过一定的结合策略形成一个强学习器,以达到博采众长的目的。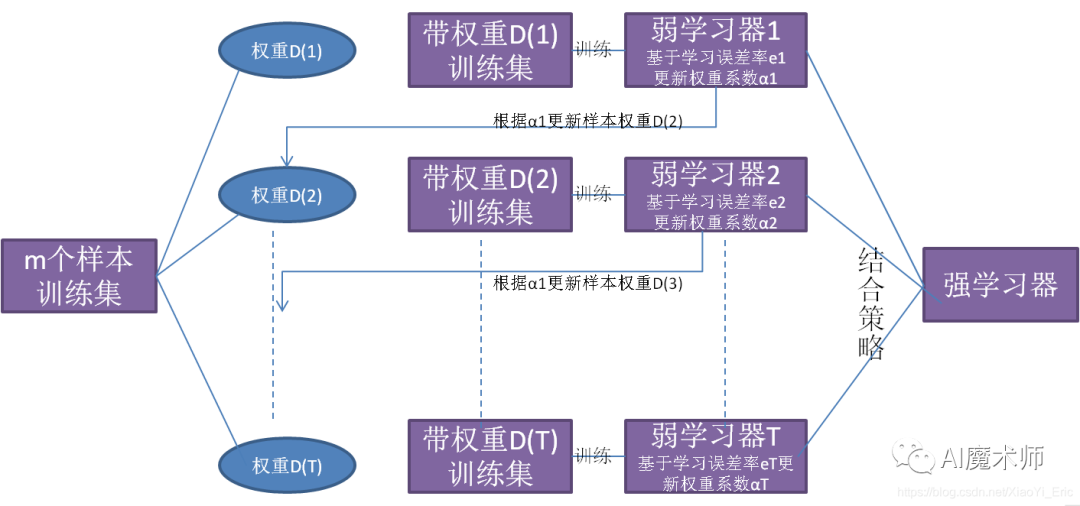
从上图可以看出,Boosting算法的工作机制是从训练集用初始权重训练出一个弱学习器1,根据弱学习器的学习误差率来更新训练样本的权重,使得之前弱学习器1中学习误差率高的训练样本点权重变高。然后这些误差率高的点在弱学习器2中得到更高的重视,利用调整权重后的训练集来训练弱学习器2。如此重复进行,直到弱学习器数达到事先指定的数目T,最终将这T个弱学习器通过集合策略进行整合,得到最终的强学习器。
GBDT全称Gradient Boosting Decison Tree,同为Boosting家族的一员,它和Adaboost有很大的不同。Adaboost 是利用前一轮弱学习器的误差率来更新训练集的权重,这样一轮轮的迭代下去,简单的说是Boosting框架+任意基学习器算法+指数损失函数。GBDT也是迭代,也使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型,同时迭代思路和Adaboost也有所不同,简单的说Boosting框架+CART回归树模型+任意损失函数。
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
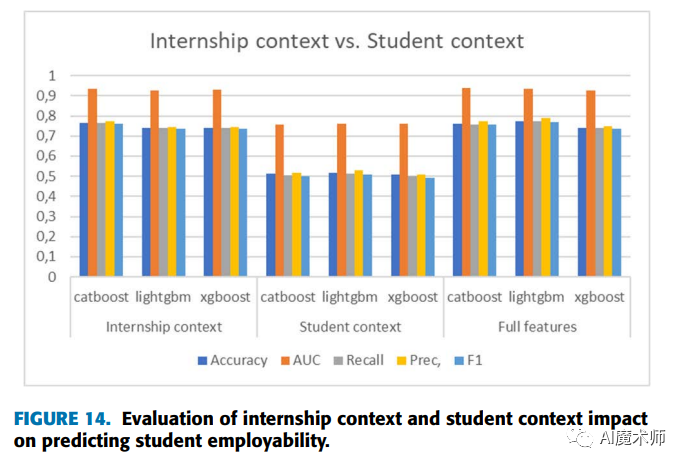
我们通过以下例子来详解算法过程,希望通过训练提升树来预测年龄。训练集是4个人,A、B、C、D年龄分别是14、16、24、26。样本中有购物金额、上网时长、经常到百度知道提问等特征。
提升树的过程如下: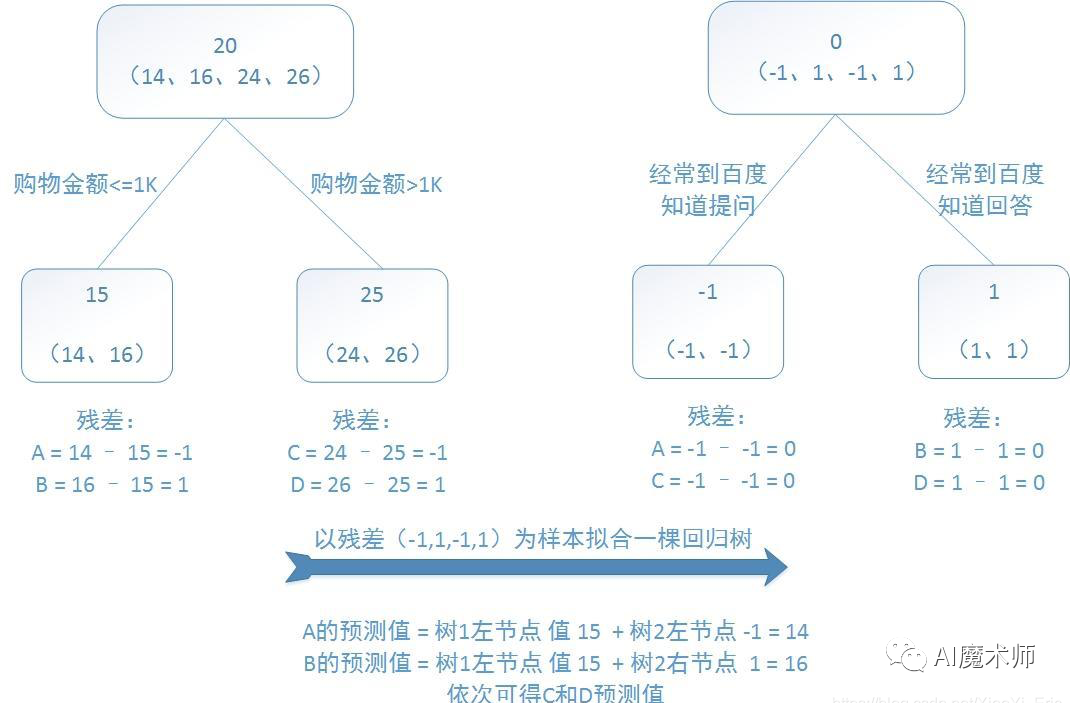
负梯度拟合
在GBDT的迭代中,假设我们前一轮迭代得到的强学习器是Ht-1(x), 损失函数是 L(f(x), Ht-1(x)) , 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器 ht(x) ,让本轮的损失 L(f(x), Ht-1(x)+ ht(x))最小,那么GBDT是如何实现让本轮的损失最小的呢?
针对这个问题,大牛Freidman提出了用损失函数的负梯度来拟合本轮损失 L(f(x), Ht-1(x)+ ht(x))的近似值,进而拟合一个CART回归树。第 t 轮的第 i 个样本的损失函数的负梯度表示为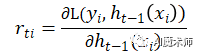
我们可以拟合一棵CART回归树,得到了第 t 棵回归树,其对应的叶结点区域Rtj ,j=1,2,⋯,J。其中 J为叶子结点的个数。
针对每一个叶子结点里的样本,我们求出使损失函数最小,也就是拟合叶子结点最好的输出值
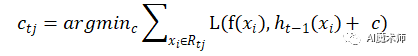
这样我们就得到了本轮的决策树拟合函数如下:

从而本轮最终得到的强学习器的表达式如下:
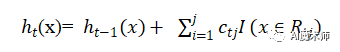
通过损失函数的负梯度来拟合,我们找到了一种通用的拟合损失误差的办法,这样无论是分类问题还是回归问题,我们通过其损失函数的负梯度的拟合,就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。
GBDT算法
回归算法
输入:训练样本 D={(, ),( , ),⋯,( , )},最大迭代次数(基学习器数量)T,损失函数 L
输出:强学习器 H(x)
算法流程:
Step1:初始化基学习器
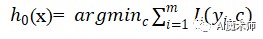
Step2:当迭代次数 t=1,2,⋯,T
(1)计算 t 次迭代的负梯度
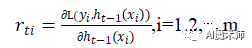
(2)拟合第 t 棵CART回归树
(3)对叶子结点区域 j=1,2,⋯,J,计算最佳拟合值
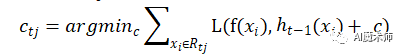
(4)更新强学习器
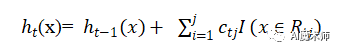
Step3:得到强学习器
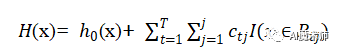
分类算法
GBDT的分类算法从思想上和GBDT的回归算法没有本质区别,但是由于样本输出不是连续的值,而是离散的类别,导致我们无法直接从输出类别去拟合类别输出的误差。
为了解决这个问题,主要有两个方法,一个是用指数损失函数,此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数,我们又有二元分类和多元分类的区别,下面简单介绍一下二元分类。
对于二元GBDT,如果用类似于逻辑回归的对数似然损失函数,则损失函数为:
L(y,h(x))=log(1+exp(−yh(x)))
其中,y∈{−1,+1}。此时的负梯度误差是
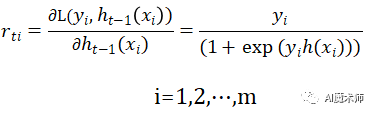
对于生成的决策树,我们各个叶子节点的最佳残差拟合值为
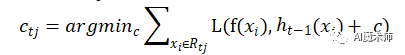
由于上式比较难优化,我们一般使用近似值代替
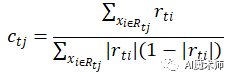
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,二元GBDT分类和GBDT回归算法过程相同。
GBDT损失函数
这里我们再对常用的GBDT损失函数做一个总结。
1.对于分类算法,其损失函数一般有对数损失函数和指数损失函数两种:

(3)Huber损失,它是均方差和绝对损失的折衷产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量。
(4)分位数损失。它对应的是分位数回归的损失函数
GBDT的正则化
和Adaboost一样,我们也需要对GBDT进行正则化,防止过拟合。GBDT的正则化主要有三种方式。
(1)第一种是和Adaboost类似的正则化项,即步长(learning rate)。定义为ν,对于前面的弱学习器的迭代
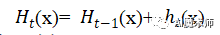
如果我们加上了正则化项,则有

对于同样的训练集学习效果,较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
(2)第二种正则化的方式是通过子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
(3)第三种是对于弱学习器即CART回归树进行正则化剪枝。
Sklearn实现GBDT算法
我们经常需要通过改变参数来让模型达到更好的分类或回归结果,具体参数设置可参考sklearn官方教程。
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.datasets import make_regression
X,y=make_regression(n_samples=1000,n_features=4,
n_informative=2,random_state=0)
print(X[0:10],y[0:10])
### X Number
# [[-0.34323505 0.73129362 0.07077408 -0.78422138]
# [-0.02852887 -0.30937759 -0.32473027 0.2847906 ]
# [ 2.00921856 0.42218461 -0.48981473 -0.85152258]
# [ 0.15081821 0.54565732 -0.25547079 -0.35687153]
# [-0.97240289 1.49613964 1.34622107 -1.49026539]
# [ 1.00610171 1.42889242 0.02479266 -0.69043143]
# [ 0.77083696 0.96234174 0.24316822 0.45730965]
# [ 0.8717585 -0.6374392 0.37450029 0.74681383]
# [ 0.69178453 -0.23550331 0.56438821 2.01124319]
# [ 0.52904524 0.14844958 0.42262862 0.47689837]]
### Y Number
# [ -12.63291254 2.12821377 -34.59433043 6.2021494 -18.03000376
# 32.9524098 85.33550027 15.3410771 124.47105816 40.98334709]
clf=GradientBoostingRegressor(n_estimators=150,learning_rate=0.6,
max_depth=15,random_state=0,loss='ls')
clf.fit(X,y)
print(clf.predict([[1,-1,-1,1]]))
# [ 25.62761791]
print(clf.score(X,y))
# 0.999999999987GBDT优缺点
优点
① 相对少的调参时间情况下可以得到较高的准确率。
② 可灵活处理各种类型数据,包括连续值和离散值,使用范围广。
③ 可使用一些健壮的损失函数,对异常值的鲁棒性较强,比如Huber损失函数。
缺点
① 弱学习器之间存在依赖关系,难以并行训练数据。
以上就是小编为大家带来的GBDT算法的简单原理讲解,如果小编有说的不对的地方,也希望大家批评指正!非常感谢各位同学们看到这里,想了解更多机器学习相关知识,可以持续关注本系列哦!
文案|杜杰鹏
指导老师|曹菁菁 赵强伟
排版 | 邓诗怡