AdaBoost算法

经过集成学习系列的首篇引入，大家是否对这篇要详细介绍的AdaBoost算法有了一些些眼熟呢？上一篇中未能详细介绍的AdaBoost算法就让我们在第二篇了解透彻吧！

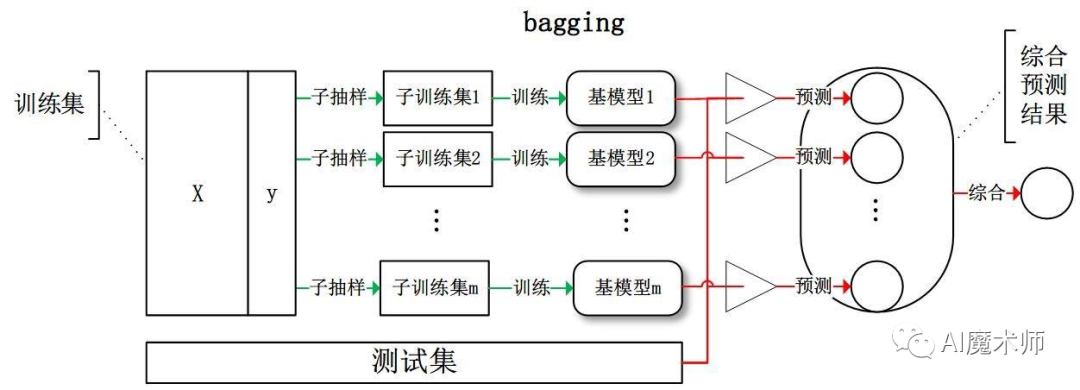
bagging与boosting

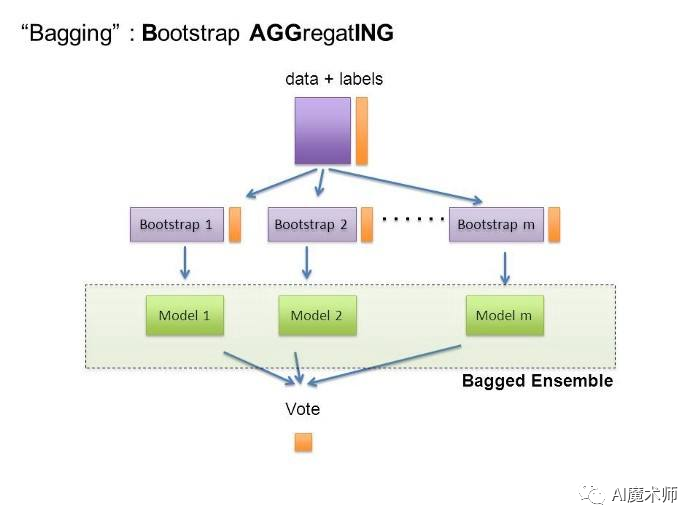
bagging

Bagging

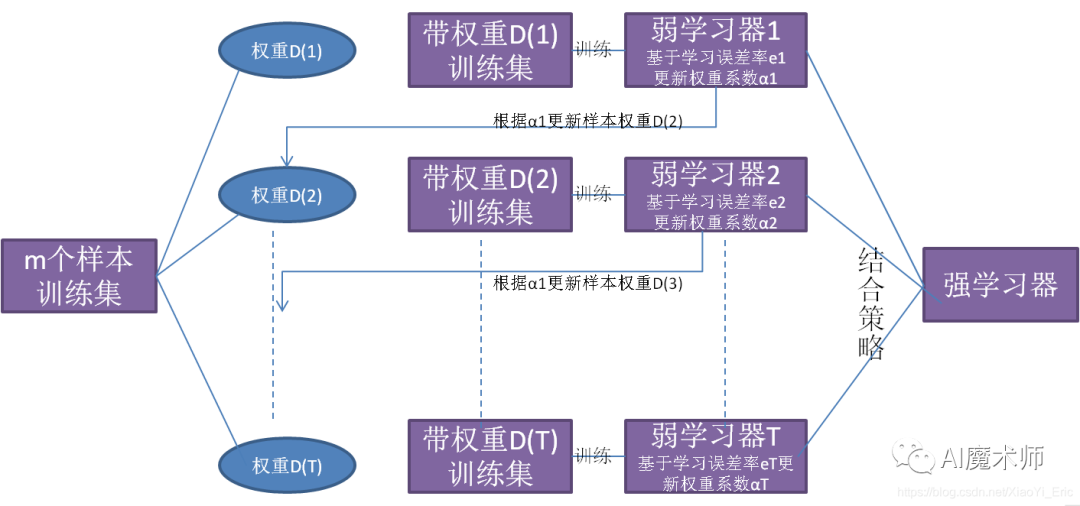
boosting算法与baging算法不同的是，学习器之间是存在先后顺序的，同时，每一个样本都是有权重的，初始时，每一个样本的权重是相等的。

首先第一个学习器对训练样本进行学习，当学习完成后，增大错误样本的权重，你可能会问，为什么要增大错误样本的权重，在分类问题中，错误的样本是算法未正确预测的结果，所以我们要增大错误样本的权重，才能在之后的预测中将之前预测错误的结果预测准确，就好比在人群中，你为什么可以一眼就认出了姚明，那是因为姚明在人群中的权重较大，，增大错误样本的权重的同时，要减小正确样本的权重，在利用第二个学习器对其进行学习，依次进行下去，最终得到b个学习器。

最后合并这b个学习器的结果，同时与bagging中不同的是，每一个学习器的权重也是不一样的。在bossting中最重要的就是Adaboost和GBDT。

adaboost算法主要步骤

主要步骤

① 从训练集D中无放回的抽样方式随机抽取一个训练子集d1，用于弱学习机c1的训练

② 从训练集D中以无放回的方式随机抽取一个训练子集d2，并将c1中误分分类样本中的50%加入训练集中，训练得到若学习机c2

③ 从训练集D中以无放回的方式随机的抽取c1，c2分类结果不一致的训练样本生成训练样本集d3，用d3来训练第三个弱学习机c3

④ 通过多数投票来组合弱学习机c1，c2，c3

boosting与bagging模型相比，boosting可以同时降低偏差和方差，bagging只能降低模型的方差，在实际的应用中，boosting算法是存在明显的高方差问题，也就是过拟合。

实例演示

import numpy as np
y = np.array([0, 1]*5) # [0, 1, 0, 1, 0, 1, 0, 1, 0, 1]

我们假设我们的原始数据是y，然后我们需要找到一个切割点，使我们预测的错误率最低，我们将预测值左边取值为0，将预测值右边取值为1，如果在第一第二个数之间进行预测，则预测结果为[0, 1, 1, 1, 1, 1,1, 1, 1, 1 ],则错误率为60.1，如果在第二个数与第三个数之间进行分割，那么预测的结果为[0, 0, 1, 1, 1, 1, 1, 1, 1, 1],错误率则为 50.1，我们找到一个错误率最低的分割点，在第七个与第八个数之间进行分割，预测值为[0, 0, 0, 0, 0, 0, 0, 1, 0, 1]，错误率为0.1*3.所以我们通过上面的结论进行推导，

通过一轮权重的更新可以发现，之前预测正确的权重由0.1变成了0.072，预测错误的权重由0.1变成了0.167，所以说，在权重更新的过程中，会增大预测错误的样本的权重，同时也会减少预测正确的权重。

利用Adaboost进行分析

import numpy as npimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.ensemble import AdaBoostClassifierfrom sklearn import treeX = np.arrange(10).reshape(-1, 1)y = np.array([1, 1, 1, -1, -1, -1,1, 1, 1, -1 ])ada = AdaBoostClassifier(n_estimators=3)ada.fit(X, y)ada.estimators_ # 可以看到adaboost是由三个决策树组成的plt.figure(figsize=(9, 6)) = tree.plottree(ada[0]) # 对第一棵树进行划分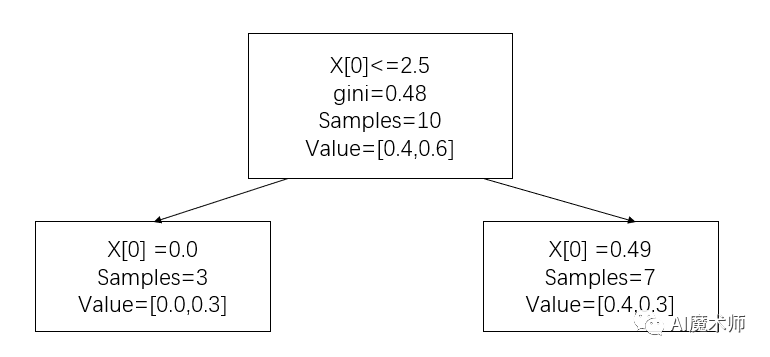

    y_ = ada[0].predict(X)

    # 计算误差率
    e1 = 0.1 * (y! = y_).sum()
    # 计算第一颗树权重
    # 随机森林中每颗树的权重是一样的，在adaboost中每棵树的权重是不一样的
    a1 = np.round(1/2*np.log((1-e1)/e1), 4)

    # 更新权重
    w2 = 0.1*n.e**(-a1*y*y_)
    # 归一化
    w2 = w2/w2.sum()

    # 得到第一个分类函数
    f1(x) = a1*G1(x) = 0.4236G1(x)
    # 进行第二轮迭代
    plt.figure(figsize=(9, 6))
    _ = tree.plot_tree(ada[1])
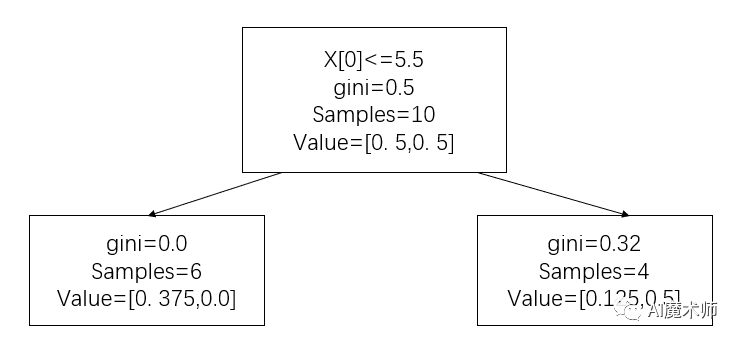![](http://www.aimagician.cn/aimagician/api/img/download/2022083020220830115042-a866.png?no_download_just_preview=1)

    # 计算误差率, 3, 4, 5预测错误
    e2 = 0.0714*3

    a2 = 1/2*np.log((1-e2)/e2, 4)
    # 计算权重
    y_ = ada[1].predict(X)
    w3 = w2*np.e**(-a2*y*y_)
    w3 = w3/w3.sum()
    w3.round(4)
    # 计算第三棵树
    plt.figure(figsize=(9, 6))
    _ = tree.plot_tree(ada[2])
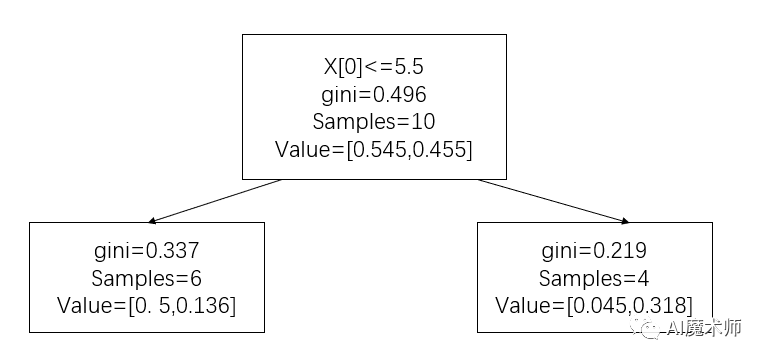![](http://www.aimagician.cn/aimagician/api/img/download/2022083020220830115050-6f93.png?no_download_just_preview=1)

y_ = ada[2].predict(X)
e3 = (w3*(y != y_)).sum()
a3 = 1/2*np.log((1-e3)/e3)

# 计算权重
# 弱分类器合并为强分类器
# 加和
# sign 符号函数，如果大于0变为1，小于0变为-1
G(x) = sign[f3(x) = sign[0.4236G1(x) + 0.6496G2(x) + 0.7514G3(x)]]
# 集成树
ada.predict(X) 
[1, 1, 1, -1, -1, -1, 1, 1, 1, -1] 
y_predict = a1*ada[0].predict(X) + a2*ada[1].predict(X) + a3*ada[2].predict(X)
np.sign(y_predict).astype(np.int)
[1, 1, 1, -1, -1, -1, 1, 1, 1, -1] # 结果与预测的完成一致