导读
最近小编接触了科学计算，为了帮助大家更好的了解和学习科学计算，诚意推出本文来简单介绍一下科学计算以及可以应用于科学计算的Numpy扩展程序库。
1. 什么是科学计算？
科学计算（Scientific Computing）即是数值计算，科学计算是指应用计算机处理科学研究和工程技术中所遇到的数学计算。在现代科学和工程技术中，经常会遇到大量复杂的数学计算问题，这些问题用一般的计算工具来解决非常困难，而用计算机来处理却非常容易。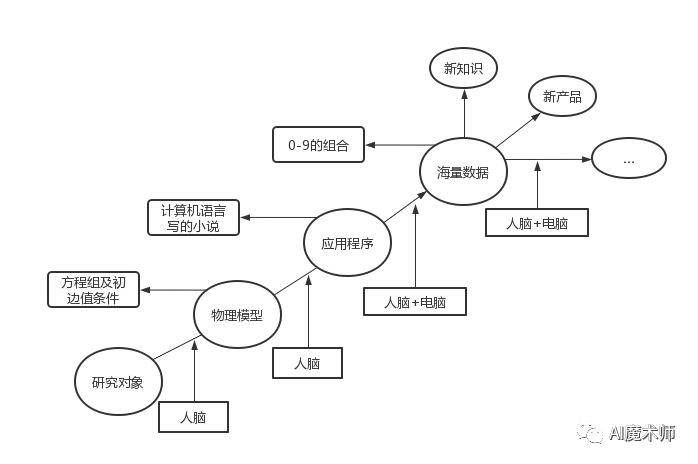
自然科学规律通常用各种类型的数学方程式表达，科学计算的目的就是寻找这些方程式的数值解。这种计算涉及庞大的运算量，简单的计算工具难以胜任。在计算机出现之前，科学研究和工程设计主要依靠实验或试验提供数据，计算仅处于辅助地位。计算机的迅速发展，使越来越多的复杂计算成为可能。利用计算机进行科学计算带来了巨大的经济效益，同时也使科学技术本身发生了根本变化：传统的科学技术只包括理论和试验两个组成部分，使用计算机后，计算已成为同等重要的第三个组成部分。
2. 科学计算主要应用领域，解决什么问题，有何特点？
1、应用领域科学计算应用领域包括科学计算、过程检测与控制、数据处理、计算机辅助系统、人工智能、多媒体、生活工作和学习等领域。
2、解决问题与理论研究相比，科学计算不仅能够处理线性问题、平衡问题，更重要的是能够处理强非线性问题、非平衡问题等，能够把科学的原理应用于解决更多、更复杂的实际问题，科学计算经常也被称为计算机虚拟实验。
3、科学计算特点一是无损。也就是说，科学计算不会对环境等产生大的影响，这一优点使得科学计算能够承担真实实验不能完成的事，例如要研究海啸的破坏、地震的破坏、核爆炸的破坏，人类不可能进行真实实验， 但可以进行科学计算， 进行计算机虚拟实验。二是全过程、全时空诊断。真实的实验，无论用多少种方法、多少种仪器，获得的系统演化的信息是非常有限的，难以做到全过程、全时空诊断。而全过程、全时空的信息对于人们认识、理解与控制研究对象极为关键。与真实实验不同，科学计算完成可以做到全过程、全时空诊断。只要在应用程序中加入相关的输出程序，在进行科学计算时，研究人员就可以根据需要获得任何一个时刻、任何一个地点研究对象发展和演化的全部信息，使得研究人员可以充分了解和细致认识研究对象的发展与演化。三是科学计算可以用相对低成本的方式。短周期反复细致地进行，获得各种条件下研究对象的全面、系统的信息。
3. 科学计算为什么选中了Numpy？
因为Numpy具有以下的优势：1.便捷，对于同样的数值计算任务，使用Numpy要比直接编写Python代码便捷得多。这是因为Numpy能够直接对数组和矩阵进行操作，可以省略很多循环语句，其众多的数学函数也会让编写代码的工作轻松许多。2.性能，Numpy中数组的存储效率和输入输出性能均远远优于Python中等价的基本数据结构(如嵌套的list容器)。其能够提升的性能是与数组中元素的数目成比例的。3.高效，Numpy的大部分代码都是用C语言写成的，这使得Numpy比纯Python代码高效得多。
结论
所以当需要大批量处理数据的时候，比如科学计算、机器学习、人工智能这些需要进行海量数据运算处理的地方，Numpy都具有很好的表现。更细一点的话，写游戏里面的物体运行逻辑时，经常涉及到矩阵、向量运算；机器人模拟环境，背后的环境反馈信息，也是靠批量数据算出来的。
4. Numpy的特性介绍
上面对Numpy进行了一些简单的介绍，下面就让我们一起来点小干货吧，分享一些Numpy的小功能。
4.1 Numpy的花式索引
花式索引（Facny indexing），利用整数数组的所有元素作为下标值进行索引，又叫数组索引。
1、整数数组索引
（1）一维数组的数组索引。
无须通过循环处理，就可以把不需要的猫猫种类通过指定数组索引过滤掉，体现了Numpy数组的强大功能，执行速度比循环处理更快。
（2）二维数组的数组索引用一维整数数组作为数组索引，生成指定行的子数组。
指定x,y坐标的数组，求指定数组对应坐标的元素，形成子数组。
2、布尔数组索引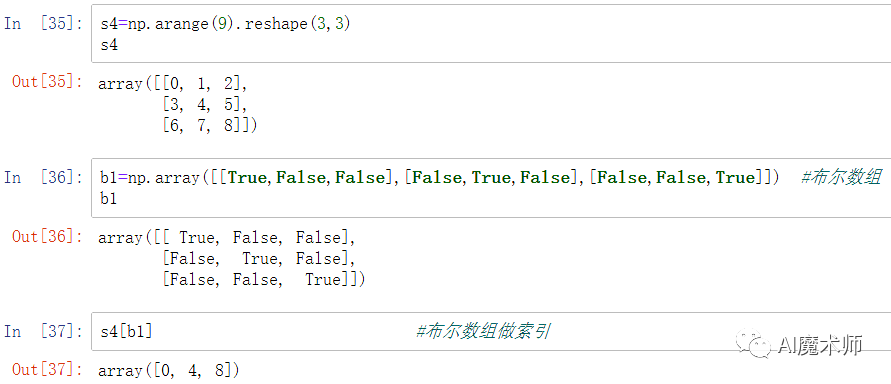
布尔索引要求布尔数组与被索引数组保持一样的形状，索引结果生成新的一维数组。
3、Numpy表达高维数组以一个三维数组为例，可以通过参数为列表的array()函数实现方式。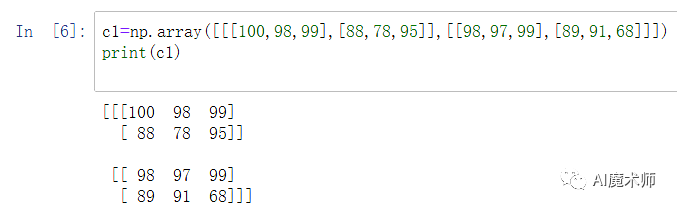
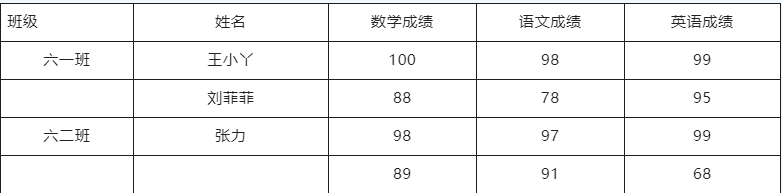表中的第一维为各课成绩，第二维为学生姓名，第三维为班级。显然三维数组代表三个层次的分类。最里层是各科成绩分类，第一维度能记录不同课程的成绩；第二层为学生分类，不同的学生有自己的各科成绩，代表第二维；第三层是班级分类，代表不同班级，它可以对应各自学生的成绩，属于第三维度。那么聪明的大家应该可以推断出来，由四种分类的数据就可以用四维数组表示啦！大家可以去亲自实践一下。
4、Numpy求解多元线性方程Numpy为求解线性方程组提高了solve()函数，例如函数solve(a, b)，a为系数矩阵，b为常数项矩阵，返回求解结果x未知数矩阵。对应线性代数的数学公式为ax=b，求线性方程组示例如下。
可以求得三个解为5，0，3。
5、Numpy与张量计算
（1）求张量张量（tensor）来源于力学，在力学、物理学里有相关应用，是数学的一个分支科学。
函数tensorsolve(a, b, axes=None)，a为系数张量数组，形状为b.shape+Q（Q为一个元组，Q=prod(b.shape)）；b为右手张量，可以是任何形状；axes可选项，a的轴向重新排序。
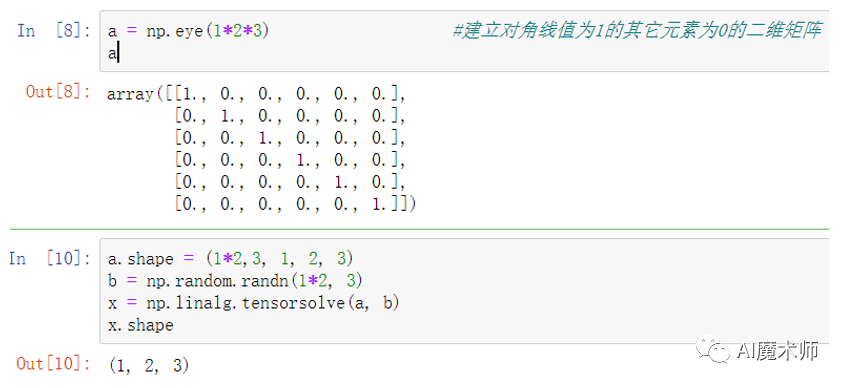
（2）求张量点积 函数tensordot(a, b, axes=2)，a、b都为具有相同大小的张量，axes可以是标量 N，也可以是具有形状 [2,k] 的整型列表。
## 5. 你还等什么呢？赶紧开始学习Numpy吧！
看了以上的一些内容，不知道大家对于科学计算以及Numpy有没有进一步的了解呢？希望能提起大家的一点兴趣，如果小编有说的不对的地方，希望大家指正哦，谢谢大家看到这里。
**-The End-**文案：杜杰鹏
指导老师：曹菁菁 赵强伟
排版：肖景昌
